
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Division and Rational Numbers Repeating Decimal Expansions · Lowest Terms · Prime Factorizations · Proper and Improper Fractions · Rationalizing the Denominator · Error · Recommended Books Repeating Decimal ExpansionsDivision is the most problematic of the basic math operations. The main reason for this is that division forces us to consider rational numbers for the first time. Rational numbers can give people fits because everyone assumes that every useful number can just be written down:
![]()
This is false. Suppose you have a rich relative who dies and leaves a $1,000,000 estate to his nine surviving relatives, including you. How much does each person get? Let's try doing a long division:
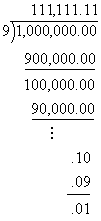
Every step does essentially the same thing in a different place, and we always wind up with 10 - 9 = 1. In the end, there is still a penny left for people to fight over, and an exact division of the estate is impossible.
Clearly, few practical people would be willing to fight over a penny, but the fact is, division failed to arrive at an exact answer. In fact, were we to put infinitely many zeros to the right of the decimal place, we would still wind up with a remainder regardless of how many steps were performed. To put this in more precise terms,
![]()
The bar over the 1 means this digit repeats endlessly. The rational number 1/9 is a perfectly legal rational number, it just happens not to have a closed (finite) representation in the decimal system. So the problem with rational numbers is that they can be hard to represent in decimals. You can say "1/9 is approximately equal to 0.11" but I can respond with "1/9 is approximately equal to 0.111" and another person can get even more exact with 0.11111111111111111. None of the approximations is exactly equal to 1/9, but we can get as close as you like. In other words, the best exact representation for 1/9 is just 1/9, the fraction.
Let's examine another case of weird representations. The following mean exactly the same thing:
![]()
How can this be? The best way to see this is to look at the difference between 1 and the decimal with n nines. This will be set up as a sequence (a list of numbers whose values depend on the position in the list)
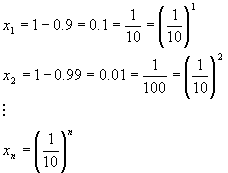
As we keep adding additional 9's onto the end of 0.9999…., the number xn gets very small. In fact, the number goes completely to zero when we extend the list of 9's out to infinity (see our discussion of limits elsewhere). Therefore, 0.99999… = 1 exactly. If the reader finds this strange or unsatisfying, the real culprit is the infinite list of 9's, not our argument.
Most of the divisions we are interested in doing don’t require long division. We’ll be happy getting fractions to lowest terms, in other words, removing common factors from both the numerator and denominator. For example, the fraction
![]()
has a common factor of 3 in both the numerator and denominator. By canceling the common 3, we reduce the fraction to lowest terms.
Prime numbers are natural numbers that have only themselves and 1 as factors. The first few primes are
![]()
These numbers are extremely important, since all other natural numbers are multiples of one or more primes. For example,
![]()
This becomes handy for reducing fractions (and other terms):
![]()
Problems with explicit, large numbers usually can be made simpler by factoring to primes and canceling common factors. This reduces division to finding fractions in lowest terms. Any further number crunching can be done with a calculator.
Proper fractions have a denominator larger than the numerator,
![]()
and represent rational numbers between 0 and 1. Improper fractions have a numerator larger than the denominator:
![]()
and represent numbers greater than 1. For most computations, improper fractions (in lowest terms) are more desirable than the "mixed" expressions (proper fractions tacked onto a whole number) like
![]()
because evaluating the improper fractions requires only a division while evaluation of the mixed representations takes a division followed by an addition. The reader can try converting both of the last two lines of numbers (they are equivalent) with a calculator to see that this is true.
Some calculations wind up with a result that looks like
![]()
with an irrational number in the denominator. This is bad because the number in the denominator doesn’t have a repeating decimal expansion nor a fractional representation. At best, this can be approximated by forcing the denominator to use only so many digits (approximation or truncation), not desirable. Instead, the above fraction is multiplied by a factor equal to one:
![]()
Now there is an irrational number in the numerator (better) and an integer in the denominator. This process is called rationalizing the denominator, and should be done whenever possible. Exceptions must be made where there is an irresolvable number in the denominator, for example
![]()
This must be left as it is, since there is no convenient number to use to rationalize the denominator. Usually, roots are the only clear candidates for rationalizing the denominator.
In mathematics, the goal is usually to work with exact numbers, in other words, to have zero error. We have pointed out several times above that error is sometimes unavoidable in practical calculations, and when this is the case, our goal becomes minimization of the error. Obviously, minimization of error is much easier if we know the source. For our purposes, error is much easier to handle in the numerator of a fraction than the denominator. Although calculus supplies much better tools to analyze error than mere algebra, we’ll attempt an elementary analysis here.
Suppose we look at a fraction with additive errors delta y in the numerator and delta x in the denominator:
![]()
We’ll presume x and y are exact and so have no error – all the error is in the delta quantities. There are several cases depending on the size of the error relative to the exact numbers. First, let’s consider the case where there is no error in the denominator. Then the above expression looks like
![]()
This case is pretty easy to analyze – the error in the whole expression is proportional to the error in the numerator. To see this in more concrete terms, choose y = 5, x = 2 and let’s consider several values of delta y.
![]()
|
|
| -1.5 | 1.75 |
0 |
2.5 |
2 |
3.5 |
The other case is not so easy. Suppose the error in the numerator is zero. Then the expression looks like
![]()
There are two problem areas with such an expression. The first is where the error in x is on the same order of magnitude as x (a rough way of saying about the same size). This is a problem because the error in the whole expression can be 100% or more. Taking the same example values as above, let’s see the effect of changing the error in x:
![]()
|
|
| -1.5 | 10 |
| 0 | 2.5 |
| 2 | 1.25 |
These examples should make it clear that error in the denominator is more serious than error in the numerator. In a future article, we’ll revisit the subject of error and use the tools of calculus to get into more detail on error handling.

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students