 Integration By Parts
Integration By Parts
- Suppose we have two functions multiplied by each other
- and differentiate according to the product rule:
- then by integrating both sides between the limits a and b
- and rearranging gives
-
-
Tricks: If one of the functions is a polynomial (say nth order) and the other is
integrable n times, then you can use the fast and easy Tabular Method:
 Tabular
Method
Tabular
Method- Suppose
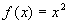 and
and 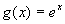 . Then if we set up a table, differentiating
f(x) as many times as it takes to get to zero and integrating g(x) as many times, we get
. Then if we set up a table, differentiating
f(x) as many times as it takes to get to zero and integrating g(x) as many times, we get
- D
|
- I
|
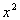 (a) (a)
|
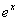
|
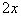 (b) (b)
|
- +
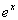 (a) (a)
|
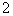 (c) (c)
|
- -
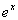 (b) (b)
|
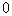
|
- +
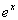 (c) (c)
|
- - notice how we alternate the signs in the “I” column. Then, multiplying rows
with like letters (which you can skip on your own paper to help make this clearer - draw
arrows instead from (a) to (a), etc.) gives the following directly as the anti-derivative:
- This method is much faster than the f-g method or the older u-v, especially for iterated
(more than once) integrals by parts (Thanks to Dr. William T. Guy, UT Austin).
 Advanced
Advanced
There is a way to extend the tabular method to handle arbitrarily large integrals by
parts - you just include the integral of the product of the functions in the last row and
pop in an extra sign (whatever is next in the alternating series), so that
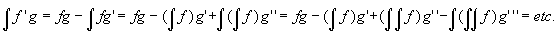
The trick is to know when to stop for the integral you are trying to do. Try it for a
few simple functions, you'll see!
 The
u - v Method:
The
u - v Method:
- This is the old standby
- which is identical to the canonical method if you set
- Many find this a lot easier to remember!
 Examples
|| 1 || 2 || 3 ||
Examples
|| 1 || 2 || 3 ||
Example 1 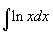
- So according to the table,
- With the u - v method,
- and
Example 2 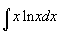
So according to the table,
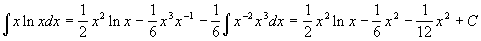
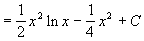

Example 3 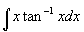
- This one is a bit more fun… from the table we have
- The last integral on the right yields to the substitution
- and
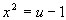 , viz.
, viz.
- which makes the final integral
So this method can be used for even very nasty integrals!
 Exercises
|| 1 || 2 || 3 ||
Exercises
|| 1 || 2 || 3 ||- These are really proofs since I give you the answers.
Use the above methods to show
1. 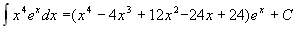
2. 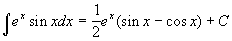
3. 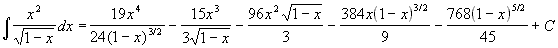
 Recommended Books
Recommended Books
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
- The classic calculus problem book - very light on theory, plenty of
problems with full solutions, more problems with answers
-
-
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus
- A simplified and updated version of the classic Schaum's Outline. Not
as complete as the previous book, but enough for most students
-
-
-
-
 Keywords
Keywords
- integral, integration, technique, parts, products, tabular, u-v
-please report any errors immediately!
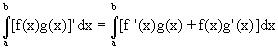
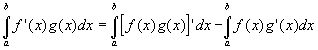
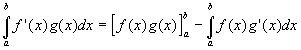
![]()
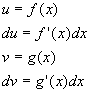
![]()
![]()
![]()
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus