
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Properties of Derivatives Linearity · Linear Combination Rule · Example using Linear Combination Rule · The Product Rule · Definition of Product Rule · Example using Product Rule · The Quotient Rule · Definition of the Quotient Rule · Example using Quotient Rule · Definition of the Chain Rule (function of a function version) · Definition of the Chain Rule (composition version) · Example of the Chain Rule · Recommended Books This article covers laws that allow us to build up derivatives of complicated functions from simpler ones. These laws form part of the everyday tools of differential calculus. Linearity Suppose f(x) and g(x) are differentiable functions and a and b are real numbers. Then the function![]()
This linearity law applies to many, many mathematical processes, so much so that we feel it is important to emphasize its nature with alternate notation.
Let us represent differentiation with respect to x by applying an operator Dx to a function:
![]()
The last notation on the right is the older, traditional notation for derivative and is included for completeness. Using this notation, the linearity law becomes
![]()
Linearity is so common that it behooves the reader to thoroughly digest this concept.
Example using Linear Combination Rule
Find the derivative of
![]()
Solution
Using linearity,
![]()
We can extend the notion of linearity to cover any number of constants and functions.
Let
![]()
Then
![]()
This rule can be applied for any finite number of terms.
This rule is used to find the derivative of a product of two functions.
Let
![]()
Then
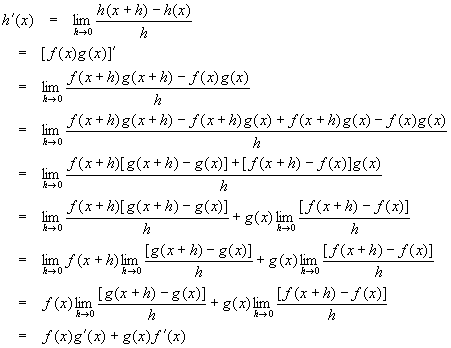
In short,
Use the product rule to find the derivative of
![]()
Solution
Here,
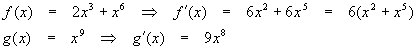
Thus
![]()
Note: Although this can be simplified, most professors (and graders!) prefer that you leave it as it is – that way, use of the product rule is clear. Also, astute readers probably observed that we could have more easily simplified h(x) algebraically first and then applied the linear combination rule. While that may be true for this example, in later sections, we will cover functions where the only practical way to do the derivative is by use of the product rule. In some cases, the easiest way to do a derivative is not the best way.
The quotient rule gives the derivative of one function divided by another. Let
![]()
And require that g(x) not be zero. Then
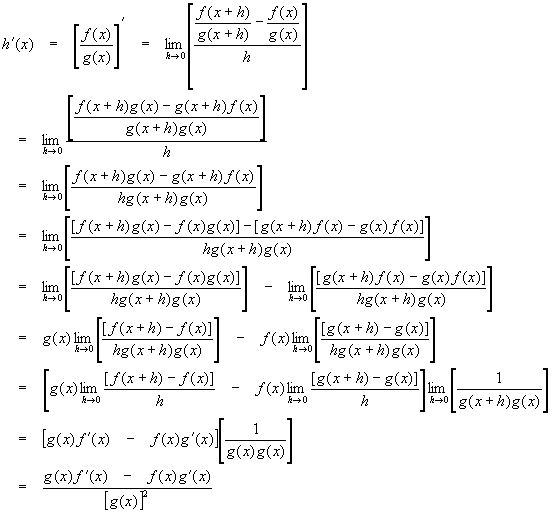
In short,
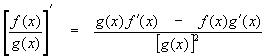 Definition of the Quotient Rule
Definition of the Quotient Rule
Find the derivative of the function
![]()
Solution
Here,
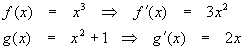
So,
![]()
As before, algebraic simplification is not always a good idea.
The chain rule is used in the case of a function of a function, also known as a composite function or as a composition of functions. There are two common notations with identical meanings:
![]()
As with linear combinations, products and quotients, composition is another tool that allows us to build more complicated functions from simpler ones. Compostions are particularly useful in the case where a given problem has so-called chained dependencies where the quantity we wish to study is a function of a second quantity which in turn depends on a third quantity. These chained dependencies arise in practical applications so often they are given the special name related rates problems.
We start with two assumptions: g must be continuous and differentiable at x0 and f must be continuous and differentiable at g(x0). Using the slope form of the definition of the derivative:
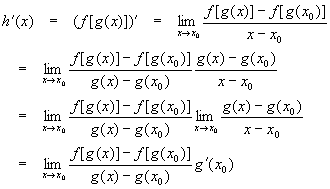
Now, if we define
![]()
Then by the continuity of g(x),
![]()
Put another way,
![]()
This allows us to make the substitution
![]()
Now we have
![]()
This is the chain rule:
![]() Definition
of the Chain Rule (function of a function version)
Definition
of the Chain Rule (function of a function version)
Using the composition notation gives
![]() Definition of the
Chain Rule (composition version)
Definition of the
Chain Rule (composition version)
Find the derivative of
![]()
Solution
We need to define the inside (g(x)) and outside (f(x)) functions:
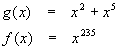
Differentiating each gives
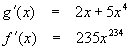
Now we apply the chain rule
![]()
Clearly, this example would have been very difficult without the chain rule - any attempt to multiply out the polynomial would take far too long and would be very likely to produce math errors.
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus
ã 1996 - 2002
Hyper-Ad Communications. All Rights Reserved.