I. Basics ![]()
Trigonometry is nothing more than how to deal with angles versus straight lines. The tricky part comes because the numbers instantly get very messy and hard to handle. Mathematics is exact by default, so we cannot cheat by clipping off digits when we no longer feel like writing them down. We have to have a decent way to handle ugly numbers. The most trigonometric way to do this is to look at several example triangles (which have “almost” nice numbers):
![]() Example 1. The 45° triangle
Example 1. The 45° triangle
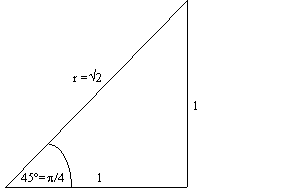 Figure 1- The 45°
triangle
Figure 1- The 45°
triangle
According to Pythagorus, ![]() . Using the
definitions of the trig functions gives us
. Using the
definitions of the trig functions gives us

![]() Example 2. The 30°/60° triangle
Example 2. The 30°/60° triangle
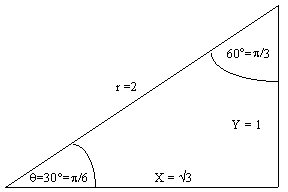 Figure 2 - The 30°/60°
triangle
Figure 2 - The 30°/60°
triangle
According to Pythagorus, ![]() . Using the
definitions of the trig functions gives
. Using the
definitions of the trig functions gives

![]() Example 3. The 15°/75° triangle
Example 3. The 15°/75° triangle
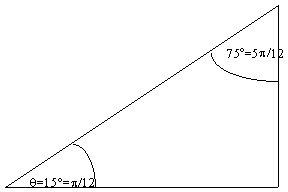 Figure 3 - The 15°/75°
triangle
Figure 3 - The 15°/75°
triangle
Now we make use of the formulas
![]()
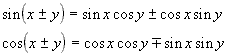
![]() Addition , Subtraction
Addition , Subtraction
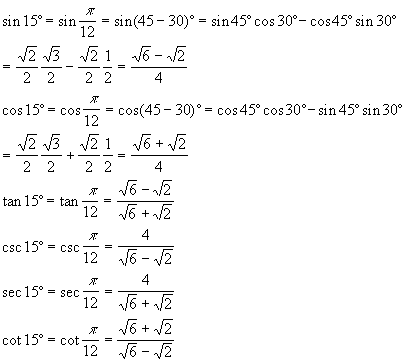
![]()
There are other triangles, but I am lazy. Let's see how far you can get with just those I've done so far and a few simple laws (so you can add and subtract and multiply and divide angles). Please note that getting 1/3 of an angle is equivalent to trisecting it, a classic impossible problem! ( Advanced - because the answer depends on solving a cubic. The answer is rather dirty-looking, anyway).
![]()
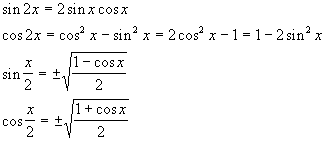
![]() Double
& half angles
Double
& half angles
And there are as many more as you care to memorize (always a mistake!). The hard part will be in coming up with smaller divisions (such as 5 degrees) without the arithmetic getting infinitely hairy. The author tried for hours and gave up!
II. Trig Identities ![]()
The only two trig functions worth worrying about are sin x and cos x ; all others are derived from these. Imagine a circle of radius r = 1 centered at the origin of the x, y plane (see Figure 1) and a point anywhere on that circle.
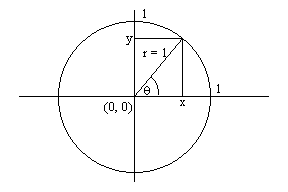
Figure 4 - The Unit Circle
Call the angle counterclockwise from the x-axis , the x-coordinate of the
point x and the y-coordinate y. Then, with r as the longest leg of the resulting triangle,
we clearly have a right triangle, so according to Pythagorus ![]()
By definition,  so,
remembering to set r = 1, we have
so,
remembering to set r = 1, we have
![]()
![]()
![]() Pythagorus'
Law, Trig version
Pythagorus'
Law, Trig version
The rest of the common trig functions come from these definitions:
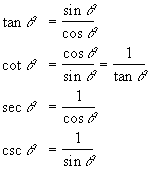
From these, we can find literally tons of “cool” trig identities: For example,
![]()
so
![]()
![]()
or
![]()
![]() Pythagorus
in terms of sec and tan
Pythagorus
in terms of sec and tan
On the other hand,
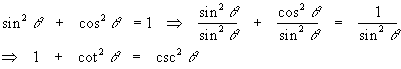
so
![]()
![]()
![]() Pythagorus
in terms of csc and cot
Pythagorus
in terms of csc and cot
If you don't mind messing with exponentials and imaginary numbers, you can easily derive the sum rule for cosine:

which proves the familiar
![]()
![]()
![]() cosine
sum rule
cosine
sum rule
If you have followed me so far, then we can take the last result and find
out that, if ![]() then
then
![]()
![]()
![]() double
angle formula.
double
angle formula.
Also, because
![]()
we also have both
![]()
![]()
![]() Double
angle formulas
Double
angle formulas
This provides us an opportunity to say
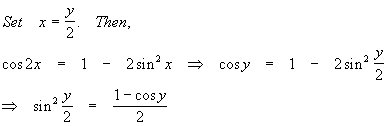
from which we get the first of the half-angle formulas
![]()
![]()
![]() Sine
half-angle formula
Sine
half-angle formula
Once you get the rules in trig form (as opposed to exp form, complicated and unfamiliar!), you can keep going until you are asleep: Let's assume that we proved
![]()
![]()
![]() Sine
sum rule
Sine
sum rule
the same way as the cosine relationship above (you do it for practice if you need to know how to manipulate those exponentials) and derive the similar formula for tangent:
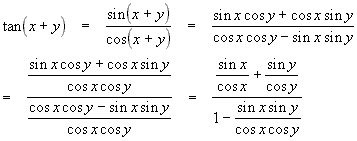
this gives
![]()
![]()
![]() Tangent
sum rule
Tangent
sum rule
There are several really good tricks to remember, they all look different in trig than they do in algebra:
![]()
![]()
![]() Difference
between two squares
Difference
between two squares
see the formula page for the rest - all algebra tricks apply directly to trig (with some cautions!).

-please report any errors immediately!