
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Chemical Equilibrium DefinitionsLe Chatelier’s Rule · The Equilibrium Constant · The Reaction Quotient · Temperature Dependence · Mole Fractions · Chemistry Index · Math Index · Chemical Equilibrium Examples I · Chemical Equilibrium Examples II · Solubility Products · Recommended Books · Advanced and In-Depth Books ·
Site Index Le Chatelier’s RuleThere is a rule called Le Chatelier’s Rule that says that, once a reaction reaches chemical equilibrium, the reaction "stops". More accurately, the forward reaction happens at the same rate as the backward reaction, and the reaction progress stops. If the reaction is not at equilibrium, then either the forward reaction predominates (reaction goes forward or to the right) or the reverse reaction predominates (reaction goes backward or to the left) until the reaction reaches equilibrium.
For a general elementary chemical reaction,
![]()
The concentrations of the reactants and products are related to each other according to
![]()
The number Kc is called the equilibrium constant, and is a function of temperature only (i.e., its numerical value doesn’t change unless the temperature changes – we’ll hold the temperature constant for now). Note the word elementary, more on that later; for now, all reactions are elementary. The stoichiometric coefficients a, b, c and d show up as powers of the corresponding reactants (and products – just call them all reactants from now on). For our example reaction,
![]()
the equilibrium constant is defined
![]()
Notice that the units of Kc in this case are M-1= L/mol.
There is another useful definition of the equilibrium constant based on pressure rather than concentration. The ideal gas law reads
![]()
Here P is the total pressure. In the case of several components, each has a partial pressure, all of which sum up to the total pressure:
![]()
For each component, we can write the ideal gas law (putting a subscript where applicable)
![]()
This works for the other components, too, and gives us the relation between the concentrations and the partial pressures. If we plug in the partial pressures in the definition of Kc above, we get
![]()
In the more general case where the reaction is
![]()
And Kc is
![]()
Then the new equilibrium constant becomes
![]()
Where
![]()
Is the change in number of moles in the gas phase. These numbers come from the balanced equation and are basically the sum of the stoichiometric coefficients of the products minus the sum of the stoichiometric coefficients of the reactants.
Problems using KP instead of Kc are solved the same way, except we are looking for the partial pressures PX instead of the concentrations [X], X = A, B, C, etc. is particularly useful for gas phase problems since the pressure is usually more convenient to measure than the concentration. Also, there is a direct relationship between KP and the Gibbs energy of the reaction, DG0rxn .
Before getting into more complicated types of equilibrium problems, it’s a good idea to look a bit more closely at why a reaction goes forward or backward. This is just a more mathematical way of looking at Le Chatelier’s rule. Suppose our reaction is not at equilibrium. We can still calculate the ratio of products to reactants, we just won’t get the equilibrium constant. This number is Qc , the reaction quotient.
For the example reaction we have been considering,
![]()
The reaction quotient is defined as
![]()
Please remember that we put "0" subscripts on our initial amounts of components to emphasize that they are not equilibrium concentrations.
Here’s how Qc should be used:
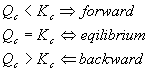
There is an equivalent notion with respect to pressure:
![]()
That works the same way
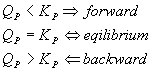
The Gibbs Free Energy of Reaction is related to the equilibrium constant KP by the relation
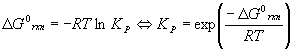
It should be noted that this equation is approximate and good for gases only. The relation between two equilibrium conditions at two temperatures is given by the Van’t Hoff equation (also approximate)
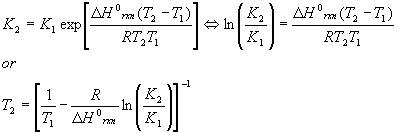
Where the K’s can be either KP or Kc ‘s.
The mole fraction of a component X is the moles of X divided by the total number of moles:
![]()
By the ideal gas law,
![]()
And so substituting for each component yields
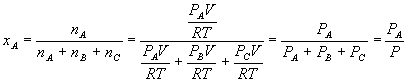
A similar relation holds for the other components, and it should be easy to prove (for our three-component system) that
![]()

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students