
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Basic Units and Measures Introduction – Unity Factors · Fundamental Units · Compound or Derived Units · Conversion of Units · Multipliers · Temperature · Afterward · Recommended Books Introduction – Unity FactorsMost calculations in science carry some sort of units, such as meters, volts, seconds or calories. We are interested in managing these units, not just to make our calculations mean something, but also as a very useful guide to how to do the calculation.
Here is a simple example. Suppose you know a bullet travels at 1500 feet per second. The number sounds fast, but is meaningless to you because you never deal with feet per second. You are more comfortable with miles per hour, so you can compare the speed of the bullet to something you know well. Convert the speed in feet per second to miles per hour.
We need to know that 1 hour = 3600 seconds and 1 mile = 5280 feet. Equalities like this are especially useful for our purposes here, since we can divide the equality by either side:
![]()
These are referred to as unity factors. They are equivalent to 1 mathematically and so we can multiply any expression by a unity factor without changing it. In effect, we are changing the notation only, not the quantity. Here is our sample calculation:
![]()
Notice how the starting quantity was just written down. Once this was done, the units in the original quantity guided the placement of unity factors (so, in particular, you can tell which factor should be on top). The units to be converted to other units must cancel (appear in the top and bottom or numerator and denominator) and be replaced by the other units.
You might also note that we started with a quantity where length is divided by time (a speed or velocity) and wound up with a quantity with the same type units – length per time. Thus, we haven’t changed the nature of the quantity. Normally, a correct conversion will end up with the same type units as it began. (Note: physicists in particular are great at wild, seemingly impossible conversions – frequency to energy to temperature, for example – but we will see that they have not really violated any laws, in fact they use laws to do the calculations.)
There are basically two systems of units still in use, with an extra sort-of system thrown in for confusion. The two systems in actual use are SI (System International), also known as the metric system, and the English system, still in use only in the United States. All calculations will one day be SI; for now, the economic muscle of the US has allowed it to be lazy about converting to the system used by the rest of the world. SI must be learned by scientists, engineers and business people; we recommend only learning the parts of the English system you need.
For our purposes here, we will treat SI units with respect and proper explanation, while English units will be used in a more familiar, cavalier manner. Non-US readers can consult an online dictionary or our glossary for fuller explanation.
The fundamental units of the SI system are mass (kilogram, kg), moles (mol), temperature (degrees Kelvin, K), current (ampere, A), length (meter, m), luminous intensity (candela, cd) and time (seconds, s). Every other quantity is expressed as a compound unit made by multiplying and / or dividing these fundamental units.
Meters are the fundamental units of length. Area is usually expressed as length x length, or length2 or L2. For example, amounts of land are usually expressed in terms of area. In the US, land is often measured in acres or square miles (mi2). Everywhere else, land is measured in square meters (m2) or square kilometers (km2). Volume is usually expressed as length x length x length, or length3 or L3. The canonical (i.e. correct according to the rules) measure of volume is cubic meters (m3), although for practical purposes liters (0.001 m3 = 10-3 m3, abbreviated "l" or "L") and milliliters (0.000001 m3 = 10-6 m3, abbreviated "ml" or "mL") are more often used.
Some compound units derive from the equations of physics. For example, length is measured in meters while the rate of change of length (or distance) with respect to time is called speed or velocity and is measured in meters per second (m/s or ms-1). The rate of change of velocity with respect to time is called acceleration and is measured in meters per second squared (m/s2 or ms-2). Force is defined by Newton’s second law (simplified) as
![]()
where m is mass (a fundamental unit) and a is acceleration (a compound unit). Using this equation as a guide we can form a new compound unit:
![]()
Thus the measure of force in SI units is the newton = kg m s-2.
Another famous equation of physics is the definition of work (also known as energy):
![]()
From this, we see that the SI unit of energy is the joule = kg m2 s-2.
There are literally hundreds of different units still in use, so practice in conversion from one set of units to another is a necessary exercise for scientists, engineers, health care workers and students thereof. Very often, data needed for a particular task is given in one set of units while work using that data needs to be done in a different set of units.
Example
One horsepower (in the original English gravitational unit) equals 550 foot-pounds per second. Find the SI equivalent of this unit (hint: watt, W = kg m2 s-3) and compare to the US definition of 746 W. One pound (really one pound-force) is the force needed to accelerate one pound-mass by one gravity. There are 0.454 kg to one pound-mass, 2.54 centimeters to the inch, 12 inches to the foot, and 100 centimeters to the meter.
Solution
First we need to deal with the pound. While there is a unit of mass called the pound-mass (lbm), the unit referred to here is really weight, a variant of force, and is more precisely called the pound-force (lbf). Using Newton’s second law, F = ma, as a guide again, we get
![]()
Note that the acceleration of gravity in English units is 32.174 ft s-2, and that the definition of a pound-force is the force needed to accelerate one pound mass by one Earth gravity. We now have an equation that will yield a useful unity factor for conversions.
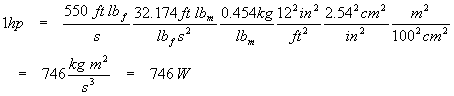
This is equivalent to the US definition to three digits of precision. Note how we handled conversion of square feet, inches, and so on: we used familiar conversion factors (such as 1 ft = 12 in) and just raised everything to the same power. Also notice that the time units (seconds) did not require any conversion; the English and metric systems both use the second as the standard of time. Also take note of how we used the units so as to cancel the ones we didn’t want and replace them with what we did want. For every unit that disappears, careful examination of the above calculation shows that the unit appears in both the numerator and the denominator and so divides to one.
The compound unit in the example above is called power, and is the rate of energy used per unit time. In simpler terms, 1 watt = 1 joule per second.
Medicine is often dispensed in units of cc’s or cubic centimeters. This allows numeric values of a dose of medicine to be expressed as 5 cc’s rather than 5.0 x 10-6m3. The cubic meter is just too big to be a convenient measure for a dose of medicine, hence the smaller, more convenient (and traditional) unit is used instead. The prefix "centi" means 1/100th. There are a whole series of prefixes that are simply multipliers of various powers of 10, used as convenient modifiers to the basic units so people can talk in terms of whole numbers from 0 to 999. The most common prefixes are:
| Prefix (abbreviation) | Multiplier |
| Femto (f) | 10-15 |
| Pico (p) | 10-12 |
| Nano (n) | 10-9 |
| Micro (m) | 10-6 |
| Milli (m) | 10-3 |
| Centi (c ) | 10-2 |
| Deci (d) | 10-1 |
| Deka (da) | 10 |
| Hecto (h) | 100 |
| Kilo (k) | 1,000 = 103 |
| Mega (M) | 1,000,000 = 106 |
| Giga (G) | 109 |
| Tera (T) | 1012 |
Express in more convenient units.
Solution
back
to top
The above calculation showed how to resolve one of the classic sticky problems of units – how to convert force and its derived compound units (energy and power) between the English and metric systems. The other common sticky issue is temperature units.
The English system uses degrees Fahrenheit, oF, as its standard temperature scale. This scale is problematic for two reasons. First, it is not really related to any natural phenomena. In particular, water freezes at 32 oF and boils at 212 oF. Second, the Fahrenheit scale is not an absolute temperature scale – there are negative temperatures using Fahrenheit which occur in the natural world and so the concept of absolute zero (the coldest possible temperature) is just an arbitrary number, -459.67 oF. The second of these two concerns can be dealt with by defining an absolute temperature scale where 0 degrees is absolute zero, and the size of 1 degree is the same as the Fahrenheit scale. This scale is called the Rankine temperature scale:
![]()
In everyday use, we just add 460 to the Fahrenheit temperature to get the Rankine temperature.
The metric system uses degrees Celsius, oC, as its standard temperature scale. This scale has a more natural origin: the freezing point of water is defined as 0oC, the boiling point of water is defined as 100oC.
Thus, this scale is related to natural phenomena, so it is relatively easy to calibrate Celsius thermometers.
Unfortunately, the Celsius scale gives absolute zero as –273.15oC, another rather arbitrary number. To fix this, the Kelvin scale was defined so that 0 K (note that K does not use the o symbol) is absolute zero and the size of 1 degree is the same as 1 degree Celsius:
![]()
Finally, we need a way to convert between degrees Fahrenheit and degrees Celsius:
![]()
![]()
Example
Normal human body temperature is 98.6oF. Find this temperature in oR, oC, and K.
Solution
Rankine:
![]()
Celsius:
![]()
Kelvin:
![]()
Note that we used the Celsius result to get the Kelvin temperature, since there was no direct Fahrenheit to Kelvin conversion given.
Further examples of units and unit conversions can be found all over these chemistry help pages. This material is fundamental to understanding chemistry, physics and most types of engineering. In most examples found even in more advanced subjects, the unit calculations will be carried out in detail.

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students