
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Quadratic Equations - Complete the Square
Introduction by Example · General Complete the Squares Method · Examples · Algebra Index · Recommended Books
One way to deal with quadratic equations is completing the square, where one takes an equation that does not quite resolve into a nice squared linear factor, such as
![]()
The method simply states that one makes it look like a perfect square on one side by adding an appropriate constant to both sides (in this case add 1 to both sides)
![]()
This equation is then factored in a straightforward way,
![]()
and the solutions are found by simply taking the square root of both sides:
![]()
Clearly these would be difficult to find by guessing. Also, note that there is a +/- symbol, indicating that there are two roots, one using the + sign and the other using the – sign. This is typical of quadratics. Since a quadratic is also known as a second-degree polynomial, it can have at most two distinct roots (which do not have to be real numbers, more on this later).
General Complete the Squares Method
To find the general method of completing the square, note that we can always start with an equation like
![]()
Since
![]()
we should examine the square term
![]()
Subtracting yields a difference of
![]()
Therefore, adding this term to both sides of our beginning equation above yields
![]()
or,
![]()
Examples · Example 1 · Example 2 · Example 3 · Example 4 · Example 5 · Example 6
Solve the following equation for x
![]()
Solution
Here b = 16, b/2 = 8 and k = -8 like so:
![]()
Plugging these numbers into our formula above gives
![]()
or
![]()
Solve the following equation for x
![]()
Solution
First, divide the entire equation by 9:
![]()
Now, b = -4, b/2 = -2 and k = 3, so plugging this into the formula gives
![]()
Solve for x
![]()
Solution
Multiply by 2 to get rid of the coefficient in front of the first term
![]()
then subtract 4 from both sides to put the equation in a form as above
![]()
Now it is apparent that b = 4, b/2 = 2 and k = -4. Plug these into the complete the square formula to get
![]()
In other words,
![]()
This equation has only one repeated root. Remember that quadratics have at most two distinct roots.
Solve for x
![]()
Solution
Even though this equation can be solved by simpler means, we are looking at using the complete the square formula, so add 1 to both sides and put in a "ghost" or zero term to hold the "x" place:
![]()
Now that the equation is in standard form, we have b = 0, b/2 = 0 and k = 1. Plugging these values into the equation yields
![]()
This is as expected, and verifies that complete the square agrees with common sense.
Solve for x
![]()
Solution
Here b = -2, b/2 = -1 and k = -5. Plugging these in gives
![]()
so that
![]()
and
![]()
This solution is interesting in that the two solutions are complex conjugates.
Solve for x
![]()
Solution
This problem is best solved by a substitution: let u = x + 2 so that x = u – 2. Putting these into either side of the equation yields
![]()
This puts the equation in standard form with b = -1, b/2 = -1/2 and k = -4, so, completing the square,
![]()
A little algebra yields
![]()
Don’t forget that we need to find x, not u, so we have one more step to go:
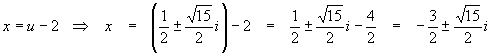
While this method might at first seem a bit complicated, it has the advantage of being very clean, avoids multiplying out a quadratic term and combining with the rest of the equation, then putting the whole thing into standard form. Substitutions like this become very important in more advanced math, and are well worth learning. Normally, they really do simplify calculations, and also often allow them to be checked for errors much more easily.

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students