A general cubic or third-degree polynomial looks like this:

We are particularly interested in finding roots of the equation

In short, we seek three numbers x₁, x₂ and x₃ so that

which also satisfy the previous equation.

There is a general method for finding roots of a cubic, but using it is quite cumbersome. We’ll tackle a simplified version of the method here. Multiplying the last equation out produces

To compare this result with the original cubic we want to solve, we must first divide by the first coefficient:

For convenience sake, we’ll abbreviate this to

Comparing coefficients gives

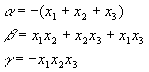
We’ll use these formulas to guess the first root.

Find a solution to

Compare the coefficients to the above formulae. We need three numbers whose sum is 6 and whose product is also 6. The only combination of numbers that fits this bill is 1, 2 and 3. We’ll need to try at least one of these roots, which naturally leads us to

Synthetic division is a way of dividing a higher-order polynomial by a lower-order polynomial. If the higher order polynomial does not divide evenly, a remainder will be left which can be expressed as a fraction. The method is similar to ordinary long division – we’ll do one of the above roots as an example.

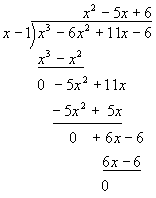
This divides evenly and so (x – 1) is a root. Some people do synthetic division with the coefficients only and leave out the powers of x. We have chosen to do it "the old way" as above, since it seems clearer.

Once the cubic is solved (i.e., after the first root is extracted), the remaining quadratic can be solved with any of the quadratic methods already discussed. As we guessed, the other two solutions are 2 and 3:

Find the roots

Comparing the coefficients shows that we need three numbers whose sum is –2 and whose product is 2. The reader might want at this point to write down several combinations of numbers that fit. This exercise is valuable for developing guessing ability, which often comes down to brainstorming possible solutions, then quickly evaluating each choice. We’re going to try –1, 1 and –2. As above, we’ll pick one of the solutions and do a synthetic division to see if it divides the cubic evenly.

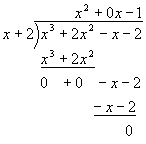
The quadratic we have left is

So our guesses turned out to be correct.

The reader can make many examples by simply choosing three (small) numbers, preferable mixing positive and negative integers, multiplying the numbers each subtracted from x in parentheses to derive the cubic, then going through the above guessing process to solve the cubic. Since the answer is known in advance, this exercise is not quite as good as starting from a totally new and unknown cubic, but the point is that the reader can make and then do many examples. After doing lots of examples, the reader will find that speed comes with practice, and solving cubics by guessing becomes very easy.