The portion of the formula under the radical is called the discriminant, and determines which of the three cases is under consideration.

In this case we have

So there are two different roots, both real numbers.

Find the roots (solve for x):

Plug the numbers into the quadratic formula

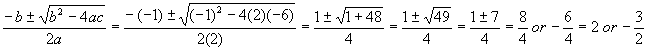
As a check, plug these solutions into a generic (parentheses or FOIL) form

Multiplying the last expression by 2 yields the above quadratic.

Find the roots (solve for x):

Plug into the quadratic formula

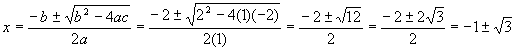
Thus the two roots are

Do a FOIL check to make sure these are correct

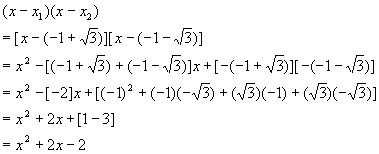
This is a good calculation to go through carefully, since it contains lots of opportunities for errors. Sticking to the FOIL method helps, as does proper use of parentheses and brackets. Instructors love putting these types of problem on exams, since they really test the students' organizational skills and attention to detail.

This is the case where the discriminant is zero

…and so the expression under the radical vanishes, leaving nothing after the +/-. This corresponds to the graph having only the vertex touching the x-axis, so there is exactly one real root.

Find the roots (solve for x):

Plug into quadratic equation:

Now do a check:

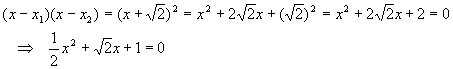
…upon division by 2. Note that it is very difficult to see that this equation is a perfect square by inspection.

Find the roots (solve for x)

Solution

Plug into quadratic formula:

As a check, multiply out the square:

A few short comments about complex numbers are appropriate here. As we saw in the Quadratic Theory section, some quadratics do not cross the x-axis at all. For example, the quadratic

never gets closer than 1 to the x-axis, and so has no real zeros at all. However, if we try to solve it anyway,

The symbol 'i' is an abbreviation for the square root of minus one, and is called the imaginary unit. Any number that includes this symbol is a complex number (not a real number). For the time being, the only thing we care about i is that i² = -1. A general complex number is usually written

where a and b are real numbers (the real part and imaginary part respectively). Every complex number has a complex conjugate

where the sign of the imaginary part is reversed. Complex conjugate pairs of numbers are interesting because their products are always real:

In fact, if either a or b is non-zero, this product is positive.

Solve for x

Plug into the FOIL to verify

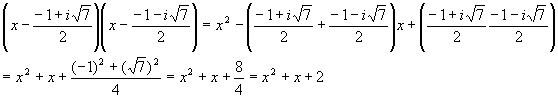
Note that we used the results from the product of complex conjugates to simplify the product of the roots.

Solve for x

Plug into quadratic formula

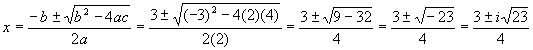
And then do a FOIL to check