
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Derivatives The Concept of Derivative · A Discontinuous Function - the Step Function · Definition of Continuity · Another Discontinuous Function - the Jump Discontinuity · Example of a Continuous Function · Differentiability · Calculation of the Derivative · Definition of the Derivative (slope form) · Definition of the Derivative (increment form) · Graphical Representation of the Derivative · Examples - Calculation of Derivatives from the Definition · Both Definitions of the Slope Are Equivalent · Magic Formula for Derivatives · Examples - Use of Magic Formula · Recommended Books The Concept of DerivativeIn addition to knowing the value of a function f(x) at a particular x, we often want to know how fast the function is changing with x. For a straight line (linear function), this is simply the slope of the line.
In the case of a curved line, the slope is different at every point. In other words, while the slope of a straight line is a constant number, the slope of a curved line is a function of x. It is our business here to learn how to find and use this function, called the derivative of f(x) and denoted f ’(x) (pronounced "f prime of x").
There are a tremendous variety of curved lines. To precisely discuss them, we’ll have to build up a certain amount of mathematical machinery. In particular, we are going to assume you have read the material on limits and worked a few examples.
The first idea to be considered is continuity. We say a function is continuous if it has no sudden jumps or "missing" points. The graph of the function is "connected" everywhere.
A Discontinuous Function - the Step Function
It is helpful to look at examples of discontinuities so we can clearly see what continuity is not. The simplest possible discontinuous function is one with a single step discontinuity:
![]()
This function is zero for x values less than zero and 1 for all x greater than or equal to zero. It has a sudden step discontinuity at x = 0. Note that in the graph below, the point (0, 0) is an open circle, indicating that that single point has been left out of the function. The point (0, 1) on the other hand is a filled-in circle and is included in the graph of f(x). This insures that the graph of the function conforms exactly with the above definition.
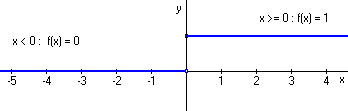
Figure 1 - The Unit Step Function (step at 0)
Rigorously, the limit of this function as x approaches 0 from below is different from the limit as x approaches 0 from above. Inspection of the graph makes this clear. This function is clearly discontinuous at x = 0. Although f(x) is continuous everywhere else, the single discontinuity makes the function discontinuous (with respect to its domain, all real numbers).
Briefly, a function is continuous at a point x0 if and only if
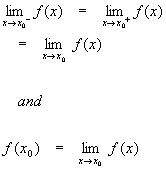 Definition
of Continuity
Definition
of Continuity
Since this concept is complicated, let’s go over the above two expressions in detail.
The first statement holds that the limit of the function as x approaches x0 from the left must be the same as the limit as x approaches x0 from the right. If this is true, then both limits are the same and we can refer to them collectively as just the limit of f(x) as x approaches x0. In other words, if the left-handed and right-handed limits are the same at a particular point, then there is a limit at that point.
The second statement says that, if the limit exists, then it must be equal to the function value at this point.
If we apply this idea to the step function above, we see that

This function fails the first condition (that the right and left limits are the same), so it fails to be continuous at 0, and so is not a continuous function.
Another Discontinuous Function - the Jump Discontinuity
There is another way a function can be discontinuous. Let’s look at a slightly different example:
![]()
This function is zero everywhere but x = 0, where it takes on the value 1. This type of discontinuity is called a jump. The graph of this function looks like this:
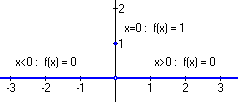
Figure 2 - The Unit Jump Function (jump at 0)
Notice that we have an open circle at the point (0, 0) to indicate that the point has been excluded from the graph and a closed circle at (0, 1) to show that this point as been included. If we perform the same analysis as above, we find that
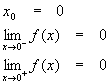
This function passes the first test of continuity since the right and left-hand limits agree. However, if we compare the function value to the limit…
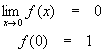
…the two values do not agree. This function is therefore not continuous at this point and so is not continuous.
Example of a Continuous Function
Now that we have considered a couple of counterexamples, we are in a better position to look at a continuous function and consider how it is different. Our example here will be
![]()
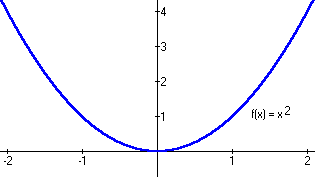
Figure 3 - Typical Continuous Function
For now, we will just assert that this function is continuous everywhere and prove it in the course of the argument which follows. The important background fact to remember here is that every real number has a real number square. Since that is true, we really don't care which number we choose, so we'll go with a generic real number. If the reader feels this is unclear, any real number can be used as the example point.
Consider an arbitrary real number x0. Calculate the limit of f(x) as x approaches x0 from the left and the right.
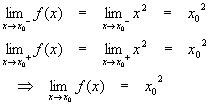
From elementary algebra, we know that x02 is defined whenever x0 is defined. In fact, we can calculate it explicitly for rational x0 and approximate it to any (finite) degree of precision if x0 is irrational. If we also note that
![]()
Then we have the function value equal to the limit at the arbitrary point x0. Since this point is arbitrary and the function value (and limit) is defined, the function passes both tests everywhere and so is continuous everywhere.
As we did above with continuity, it is instructive to consider a function that is not differentiable so we can contrast it with functions that are differentiable.
Consider the absolute value function
![]()
The graph of this function looks like this:
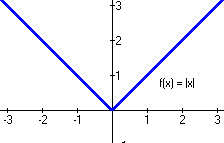
Figure 4 - The Absolute Value Function
The interesting point is at zero – this function has a sharp, sudden kink to it. By inspection, it is pretty clear that the slope of this function to the left of zero is m = -1, but at zero or above the slope is m = +1:
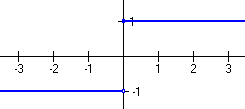
Figure 5 - Derivative of Absolute Value Function
The slope is not continuous at zero – we say that this function is not differentiable at zero. When we look at the definition of the derivative below, it will be easy to see that the left and right hand limits of the derivative function must match at a point in order for the derivative to exist at that point. Moreover, the value of the derivative must match what we expect from the limits to get a properly defined derivative at that point. In other words, the derivative must be a continuous function.
From elementary algebra, we have the familiar formula for the slope of a line given two points on the line (x1, y1) and (x2, y2):
![]() Definition of Slope
(two-point form)
Definition of Slope
(two-point form)
Were we to use functional notation with this formula, in other words use the substitution
![]()
to get
![]() Definition of Slope (functional form)
Definition of Slope (functional form)
then it becomes a bit clearer that we are actually dividing an increment in the function value by an increment in the variable. As it stands now, this number is the same everywhere for a straight line because the ratio of the rise to the run is always constant. For a more general function, the value m above depends in general on both x1 and x2; different choices of these two numbers will give different values of m.
What we would like to do is find the slope of a function at a point x0 as a function of that point. In that case, we will redefine our points a bit, to allow us to better calculate this number.
Put
![]()
so that the slope now looks like
![]()
If we let x approach x0, in other words, take the limit, we have the definition of the derivative:
![]() Definition
of the Derivative (slope form)
Definition
of the Derivative (slope form)
We can do this a different way and get the same results. This time, make the following substitutions in the functional form of the slope definition:
![]()
Substituting these into the slope formula gives
![]()
In this last expression, x0 is (again) the point where we wish to find the slope and h is now an increment (either positive or negative) that defines how far away from x0 we move to get another point to calculate the slope. You can think of h as a dial that we can turn to get various approximations of our slope. The smaller the absolute value of h, the closer we get to our derivative. However, since h appears alone in the denominator, we cannot just substitute zero – the expression would then be undefined.
It should come as no surprise that we use the limiting process to "dial down" the value of h. This then becomes the alternative definition of the derivative:
![]() Definition of the Derivative (increment form)
Definition of the Derivative (increment form)
Graphical Representation of the Derivative
A picture of this process might make things a bit clearer.
Here we consider the function x2 (graphed in blue). First, we take two points on the x-axis, x0 and some other point x. For each x value find the function values f(x0) and f(x). This gives us two points on the graph of x2: (x0, f(x0)) = (x0, x02) and (x, f(x)) = (x, x2). Draw a straight line through them (graphed in red).
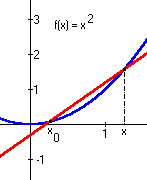
Figure 6 - Construction of Derivative
Imagine how the line graphed in red changes as we move x a little closer to x0. The slope becomes a bit less steep, and the y-intercept of the line moves up a little bit. When x is moved all the way over so that x = x0 the graph looks like this:
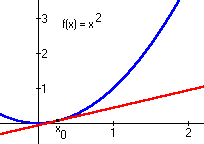
Figure 7 - Derivative as Tangent Line
Now the red straight line touches the graph of x2 at only one point (x0) and has the same slope as the curve at this single point only. We call this straight line the tangent line at x0. The slope of this tangent line is the value of the derivative of x2 at x0.
Examples - Calculation of
Derivatives from the Definition
The derivative of a straight line: f(x) = mx + b
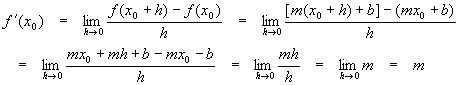
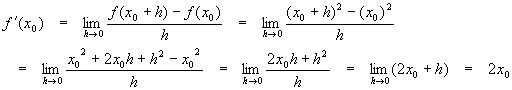

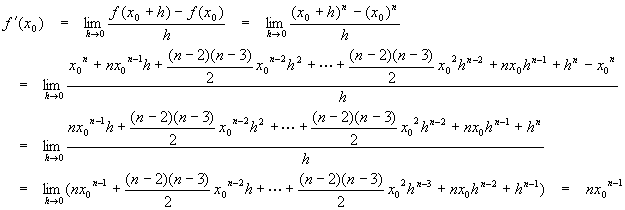
![]()
A more detailed study of this formula can be found in the section on advanced algebra.
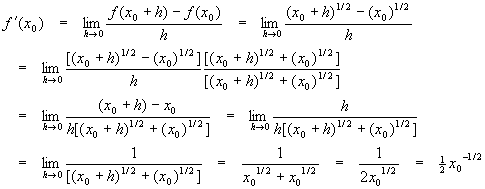
Both Definitions of the Slope Are Equivalent
We should show that each of the forms of the definition of the slope give the exact same result. In the examples above, we found via the "increment form" of the slope that
![]()
Let's try the same calculation with the "slope form" of the definition of the derivative to be sure it gives the same result.

As expected, the results are the same. You should practice using both forms until proficient with the calculations, then you can choose the form which best suits the problem you are working.
Inspection of the preceding examples suggests (but does not completely prove) the following formula:
![]()
We showed the calculations above for integer values of n and one example of a rational value of n. The formula is good for general n’s (any real n), but the proof of the most general case is too involved for our purposes here. Use of this formula considerably speeds calculation of derivatives for powers of x.
Examples - Use of Magic Formula
![]()
![]()
![]()
We will use this formula whenever possible since it is much easier to use than the definition. The reader should be cautioned that the magic formula does not work everywhere. In particular, the magic formula does not work for exponential functions.
Exponential functions raise a positive number to the power of x, rather than x raised to a number power:
![]()
Fortunately, we do have ways of dealing with exponential functions elegantly and will cover them later.
When in doubt, start with either version of the definition. The definition is guaranteed to be correct, but not guaranteed to produce manageable algebra.
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus
ã 1996 - 2002
Hyper-Ad Communications. All Rights Reserved.