
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Limits - Formal Definition and Proofs
Formal definition of the limit · Handling infinity on the x side · Handling infinity on the y side · Handling infinity on both sides · Summary - Table of Cases · Recommended BooksA limit is the value of a math expression as one of its variables approaches a particular point. Here is a trivial example
![]()
This reads "the limit of the square root of x, as x approaches 4, is 2". All that is needed with this limit is straight substitution of the number 4 for x. Since this example is very simple, it is likewise not very useful, but it does show the basics of the notation. Limits are much more useful in situations where ordinary substitution breaks down:
![]()
Here, it is not really proper to substitute infinity for x - infinity is not a number, it is a concept. What this statement is really saying is that as x gets (arbitrarily) large, 1/x gets (arbitrarily) small. There is a formal way of "proving" this, although most calculus students find the formal proof even more difficult to understand than the simple limit statement.
back to top Formal definition of the limit (finite x, finite y)The expression
![]()
Means that for every
e > 0 (small), there is a d > 0 (small) such that | x - x0 | < d implies | f(x) - y0 | < e .First, let's go through this analytically (i.e., with formal mathematical analysis) to get a feel for the symbols and what they mean. Take the easy case above as an example, so that x0 = 4, y0 = 2 and
![]()
All that is needed is to tie one absolute value inequality to the other with valid mathematical steps. In this case, it is a little better to start with the result and work backward:
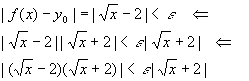
According to the algebra formula
![]()
When we replace x with x1/2 and a with 2, we get
![]()
Therefore
![]()
(* this is called the triangle inequality, more on this later) which means, if we set
![]()
then
![]()
This proves the theorem and demonstrates use of the formal definition of the limit. If this is still a little abstract for you, here is a specific example.
The above says: if x is no farther away from 4 than
d = 0.01, then y = x1/2 is no farther away from 2 than whatever e(d) happens to be. We have to calculate it from the above equation (and we use the quadratic formula to get the solution for the polynomial):
Plugging in
d = 0.01, we get e(d) = e(0.01) = (4 + 0.01)1/2 – 2 = 2.002498… - 2 = 0.002498… In other words, pick some value of x between 3.99 and 4.01 and y will be between 1.9975 and 2.0025 (approximately). Let’s try it: Pick x = 4.001 which is clearly within the limits for x, and so puttingthe difference in makes
d = 0.001 so e(d) = e(0.001) = (4 + 0.001)1/2 – 2 = 0.00025, or y = 2 + 0.00025 = 2.00025, which is clearly between the above limits for y.While this discussion is a bit much for business calculus students, those studying calculus for science and engineering typically have to know how to do proofs like the one above. Math classes rarely stick numbers into these formulas, but we do it here to show that the formulas indeed do work.

Now that we have done a little analytical and numerical work, a picture tells a thousand words. Take a close look at the graph. Notice that x0 and y0 are connected through the graph of the function f(x) by a solid line - this indicates that y0 = f(x0). Around x0 are "error regions" of width
d, and around y0 = f(x0) are error regions of width e = e(d). Just as f(x) "controls" the value of y0 given x0, the function f(x) also "controls" the size of the error regions around y0 = f(x0), e, given that the error regions around x0 are of size d. Squeezing the error regions around x0 tighter (which is the same as making d smaller) forces the error regions around y0 to get tighter also (which is the same as making e smaller)
All the important proofs involving limits simply require finding creative ways to get from the inequality on the x side to the inequality on the y side, or vice-versa. A little bit of algebra, some examples, some tools such as the quadratic formula, the triangle inequality and some others are all that is needed to do the proofs. It takes a bit more effort (plowing through the above example very slowly, taking extreme care that every single step is understood with no gaps) to understand the proofs well enough to see how they really do show the guts of how limits work.
Example Use of the formal definition of the limit
Prove that
![]()
By use of the formal definition of the limit.
Proof
Here x0 = 3, y0 = 9 and f(x) = x2. Plugging these into the result (y) side inequality,
![]()
Notice that the inequality is now asymmetric, which doesn't hurt us too badly. We really need to require
e << 1 (which is also not a problem - both e and d are always very small numbers), so that all the quantities in the inequality are positive and greater than 1. Then we can just take the square root of each expression![]()
The question remains, "Which of the expressions on either side of x - 3 should we pick?" We can't use both. The answer is to use the one with the smaller absolute value:
![]()
With this definition of
d, we can guarantee that | x - 3 | < d implies that | x2 - 9 | < e. back to top Handling infinity on the x sideA slightly different formal definition of the limit is used when x goes to +/- infinity, since we really cannot subtract x from infinity or vice versa - remember, infinity is a concept, not a number. Formally, the expression
![]()
Means that for every M > 0 (large) there is a
e > 0 (small) so that x > M implies | f(x) - y0 | < e.Example Use this formal definition of the limit to prove that
![]()
Proof
Again we start with the y side and work backwards to the x side. Since y0 = 0, we have
![]()
So setting M=1/
e gives use a lower bound on x which works. back to top Handling infinity on the y sideThis is a limit where x tends toward a finite value but y gets infinite. Formally, this is a limit of the form
![]()
Defined for every
d > 0 (small) there is an N > 0 (large) so that | x - x0 | < d implies f(x) > N.Example Use this formal definition of the limit to show that
![]()
Proof
This time it's better to proceed from the x side to the y side
![]()
Not only does x get infinite, so does y. The limit will look like
![]()
And is defined for every M > 0 (large) there is an N > 0 (large) so that x > M implies f(x) > N.
Example Use this definition to show that
![]()
Proof
![]()
In each case, a connection is established between bounds for each side. To summarize, here are the cases we have considered.
Case (x side / y side) |
Proof tries to find |
Proof usually easiest |
| Finite / finite | d(e) | Backwards ( y side to x side) |
| Infinite / finite | M(e) | Backwards ( y side to x side) |
| Finite / infinite | N(d) | Forwards (x side to y side) |
| Infinite / infinite | N(M) | Either way |
It should be noted that whether a proof goes forwards or backwards really has to do with irreversible steps in the proof, rather than the side from which one starts. The above is "advice" rather than a hard and fast set of rules. In advanced math, the implications go in the direction of more to less general, so that a more general statement implies a less general statement. This requires considerable practice to do well, and is really only an issue for those who will have to continue learning proofs into the advanced stages, in other words, mostly mathematicians, scientists and engineers who intend to publish theoretical papers. Everyone else can afford a bit of laxity in their proofs, and need learn the art of proofs only as needed to satisfy math professors.
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus