
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
The Sine Function Introduction · Graph of the Sine Function · Periodic Functions · Odd Functions · Recommended Books IntroductionFrom our previous discussion of the unit circle, we know that the y-coordinate of any point P on the circle is given by the sine of the angle q between the positive x-axis and the line between the origin and P.
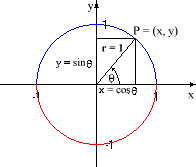
If one imagines the point P moving around the circle counter-clockwise starting from the point (0, 1) on the x-axis, the y-coordinate of P (which is y = sinq) goes from: y = 0 at q = 0; to y = 1 at q = 90o = p/2; to y = 0 again at q = 180o = p; to y = -1 at q = 270o = 3p/2; then back to y = 0 at q = 360o = 2p. Notice that the starting and ending points are the same; in other words, 0o = 360o = 0 = 2p (last two expressed in radians).
Were we to show several circuits around the circle as a graph of the vertical displacement (y-coordinate) vs. the angle, it would look like this:
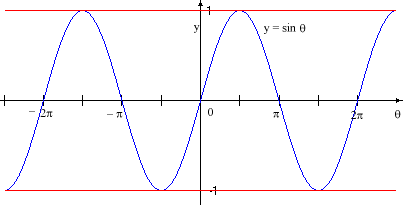
The most obvious single feature of this graph is that it is periodic (a portion of the graph is repeated endlessly). In fact, the period of this function is T = 2p, so any portion of the graph that includes a full period repeats. In particular, the segments
![]()
and
![]()
both contain one full period, and either can be used as the repeating segment of the graph. The reader is cautioned to notice a tiny but very important detail here – I have removed the rightmost endpoint from both segments. This endpoint would be included in the next repeating segment: [p, 3p) or [2p, 4p), respectively. Pickiness about such details now will save confusion later.
We have two different candidates for the basic, repeating segment of sine. Which should be used? Use the period that is more convenient for the problem we have to solve.
A periodic function f(x) has a constant number T associated with it, called the period, so that for every x in the domain of f,
![]()
In the case of sine, T = 2p, so that
![]()
This is true for all real q. For example,
![]()
For this reason, it is only necessary to study a single period of the function in order to know its behavior everywhere. Since we are concerned with angles starting from the x-axis, we will use the period [0, 2p) as our sample period and ignore the entire rest of the real line (for now).
An odd function f(x) has the property
![]()
Sine is an odd function, so
![]()
Again, this is true for all real q. For example,
![]()
