
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Chemical Equilibrium – Solubility Products
Solubility Product · Soluble or Insoluble? · Recommended Books · Chemical Equilibrium Definitions · Chemical Equilibrium Examples I · Chemical Equilibrium Examples II
Now we consider some problems in solution equilibrium. There are two broad cases to be considered - very soluble salts such as NaCl which dissociate 100% upon addition to water
![]()
and insoluble salts which barely dissolve and always have solid precipitate present. A typical example is
![]()
This describes lead (Pb+2) and sulfate (SO4-2) ions dissolved in solution, the aqueous phase (aq), in equilibrium with the sparingly soluble solid (s) salt PbSO4. Similarly to the other chemical equilibrium problems we have seen, there is an equilibrium constant, Ksp, defined as
![]()
As long as solid PbSO4 is present, the solution is not only at equilibrium, but is also saturated (contains as much dissolved salt as it can hold).
Example:
Solid PbSO4 is placed in water and the resulting mixture is left alone for a long time. There is still solid remaining after the waiting time, and the solution is presumed to be in equilibrium. What are the equilibrium concentrations of the two ionic species,
Pb+2 and SO4-2 ? The value of Ksp is 1.8x10-8 M2.
Solution:
Write a start-change-finish diagram, assuming the amount of solid lead sulfate is infinite
(subtracting the small amount that dissolves doesn’t matter):
| Component | Pb+2 |
SO4-2 |
PbSO4 |
| Start | 0 | 0 | N/A |
| Change | + x | + x | - x |
| Finish | x | x | N/A |
Plugging in to the equilibrium equation gives us
![]()
So
[Pb+2] = [SO4-2] = x = 1.34x10-4 M.
As you can see, these types of problems are usually much easier to solve algebraically than the chemical equilibrium problems considered earlier.
Example
Solid Cadmium Arsenate, Cd3(AsO4)2 , is in equilibrium with its own saturated solution. The salt has a solubility product constant Ksp = 2.2x10-32. What are the concentrations of the two ionic species Cd+2 and AsO4-3 ?
Solution
Notice that the stoichiometric coefficients are important, since they are not all one as in the previous example, so write a chemical reaction first
![]()
Now, write a start-change-finish diagram with the same assumptions as before, but notice how the stoichiometric coefficients change the diagram
| Component | Cd3(AsO4)2 |
Cd+2 |
AsO4-3 |
| Start | N/A | 0 | 0 |
| Change | N/A | + 3x | + 2x |
| Finish | N/A | 3x | 2x |
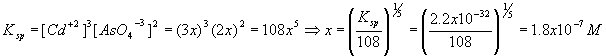
Therefore,
[Cd+2] = 3x = 3(1.8x10-7) = 5.5x10-7 M
[AsO4-3] = 2x = 2(1.8x10-7) = 3.7 x10-7 M
There are rules to help decide whether a compound is likely to be soluble or insoluble in water. These are almost always listed in any good freshman chemistry text. Here's a drastically simplified rule: The farther apart the chemical species are on the periodic table, the more likely it is that the salt is soluble. This rule is not very helpful when talking about compound ions like NH4+ (all compounds soluble, by the way) or SO3-2
(depends on the cation whether soluble or not), but does provide some intuition for simple salts such as NaBr (soluble), Cu2S (insoluble) and AuI (insoluble).

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students