
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Chemical Equilibrium Examples ITypes of Problems · Start-Change-Finish Diagrams · Trial and Error Solution · Adding or removing one component · Chemistry Index · Math Index · Chemical Equilibrium Definitions · Chemical Equilibrium Examples II · Solubility Products · Recommended Books · Advanced and In-Depth Books · Site Index
Introduction to Chemical Equilibrium: Types of ProblemsTake a simple gas-phase chemical reaction, like:
![]()
Which we’ll abbreviate to
![]()
And ask questions like:
There are other, more subtle questions that can be asked, but these five cover the essentials.
Example Simple equilibrium calculation
Suppose for the above reaction we keep the equilibrium concentrations of the reactants at [PCl3] = [A] = 0.5 M and [Cl2] = [B] = 0.07 M and the temperature at 400K, so that Kc = 96.2 M-1. What is the equilibrium concentration of the product, PCl5 ?
Solution Solve the equation for the quantity we want:
![]()
Then simply plug in the numbers
![]()
Now, we can complicate this problem just a bit by having the concentrations of A and B be initial, rather than equilibrium, quantities. The problem is different because we put some of A and B into the reaction vessel, and some of each reacts (i.e., goes away) to form some C. The initial concentration of C is zero.
The technique in this case is to set up a start-change-finish diagram
| Component | A | B | C |
| Start | [A]0 | [B]0 | [C]0 |
| Change | - x | - x | + x |
| Finish | [A]0 - x | [B]0 - x | [C]0 + x |
The finish line is found by adding the start and the change entries in each column. We are assuming the reaction goes forward when we used a "-x" for A and B; if we are wrong (the reaction actually goes backwards) the only thing that will happen is that x will be negative (which is no big deal). The entries on the finish line are the equilibrium concentrations of each component:
Plugging these into the equilibrium equation yields
![]()
If Kc , [A]0 , [B]0 , and [C]0 are given, then this equation becomes simply a quadratic equation in x and is solved via the familiar quadratic formula
![]()
Example Basic Start-Change-Finish problem
Suppose we start with equal initial concentrations of A and B, [A]0 = [B] 0 = 0.14 M, and do the same reaction at the same temperature so that that Kc = 96.2 M-1. What is the new equilibrium concentration of the product C ?
Solution It’s easier to do algebra with symbols than numbers, so let’s call a = [A]0 = [B] 0 = 0.14 M, and b = [C]0 . Since there is no C initially, [C]0 = 0 and the equation becomes
![]()
According to our algebra formulae, (
a - x)2 = a2 - 2ax + x2 and so![]()
This last expression is in quadratic form with
Note that the units come out so that every quantity is in molarity – this is correct since x must be in units of molarity. Putting these numbers into the quadratic formula gives us
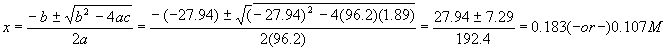
The quadratic formula gives two solutions – which is the correct one? Notice that the first solution is larger than the initial amount of reactant – so even if 100% reacted, the most product we could get is 0.14M, so we reject that solution and take
The last number is our desired answer; notice we solved for all the other numbers in the problem, too – this is a real good habit, since you maximize learning for each problem solved. Another good habit is to run a check on the final numbers by calculating Kc again:
![]()
The answer is a little different from the original number, because we rounded the answers in the denominator. This is normal, and shows how rounding can introduce error. For our purposes here, this is close enough. When precision matters more, we’ll be more careful.
There are several things that should be pointed out now; the most important is the algebra got complicated. This will get worse in other problems we consider below, so the reader is advised to go slow and be extremely careful. Mistakes in algebra are easy to make and hard to find. The other important observation is that organization and neatness drastically improve your chances of getting the answer right the first time, and make it much simpler to find mistakes when you make them. You will make mistakes, so do yourself a favor and make these problems look good on paper. You’ll be very glad you took the extra effort.
Now, let’s take a look at what happens when we increase the precision of the calculation: in the above calculation, we could have used more digits:
![]()
With this increased precision, we get for the equilibrium constant
![]()
The answer is worse when we used more digits! The lesson here is that increased precision doesn’t necessarily mean more accurate answers. Use the rules of significant digits carefully and don’t worry too much if the answers are a little different (a few percent error, say less than 5%, is OK). There are ways to get better answers by careful choice of calculation method. Suffice to say that small errors in small denominators can cause relatively large errors – this is a good place to be cautious.
back to top Trial and Error SolutionSuppose the errors in Kc got you nervous – you are not comfortable with errors you cannot explain. Here’s a way to get arbitrarily good precision with the same calculation. This method is especially important for engineering and science students – it’s called trial and error or successive approximations. It’s a bit involved, and is best done either on a programmable calculator or programmed with a computer (if you know how to do that).
Start with an expression we found above:

This is important because x is by itself on the left and is also in an expression on the right. The expression on the right is a weaker function of x (has a smaller power of x) so successive calculations of x are likely to converge (get closer together). We’ll guess a value for x, plug it in on the right, do the calculation, get a new x, put it in on the right side again, do the calculation again, get a new x, and keep going until the value of x is constant for the first four significant digits. A good starting value for guessing x would be 0.
Therefore,
![]()
Put this in for x and we get
![]()
Do it again (x is not yet constant!)
![]()
Do it again
![]()
And again
![]()
One more time
![]()
The input value of x is the same as the output value. Stop the iterations now. Using this value of x, the equilibrium concentrations become
And the calculated value of the equilibrium constant is
![]()
Trial and error, although a bit of a pain, is the preferred way to do calculations which are sensitive to precision such as this one. For most chemistry exams, this is too time-consuming and will NOT be necessary, but for situations where you need good quality numbers, this is how to get them.
back to top Adding or removing one componentThis answers the second of our original questions posed in the introduction. Suppose we started with the system we just finished at equilibrium. Now, we add some extra A – what happens to the equilibrium? According to Le Chatelier’s Rule, equilibrium should move to the right – in other words, some more C will be made and a corresponding amount of A and B will be consumed.
Example Changes in concentration
To the above equilibrium system we suddenly add an extra 0.0500M of A. What are the new equilibrium concentrations of each component?
Solution Set
a to our starting (old equilibrium) concentrations of A and B: a = 0.0333M. Set b to be the initial amount of C: b = 0.1067M, and let g be the extra added amount of A: g = 0.0500M. We expect the reaction to shift to the right since we’re adding stuff on the left (Le Chatelier’s principle (at least partially) undoes whatever we do to the equilibrium), so x of both A and B will react to form x more C. Setting up a new start-change-finish diagram,| Component | A | B | C |
| Start | [A]0 = a + g | [B]0 = a | [C]0 = b |
| Change | - x | - x | + x |
| Finish | a + g - x | a - x | b + x |
Now, plugging these into the same definition of the equilibrium constant
![]()
Since in this case we can accept a little error, we’ll go for a straightforward solution with the quadratic formula
![]()
The best way to handle these coefficients is to calculate them now
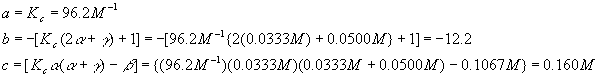
Notice that each term in the equation has units of molarity. Using the quadratic equation,
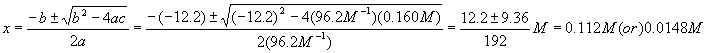
Which answer should we choose? If we pick the first solution, we wind up with a negative value for the equilibrium concentration of A, which is nonsense, so pick the second solution. Therefore,
![]()
Close enough. The reader can probably now try a problem where a little bit of B is added instead of A, or try adding a little bit of C and do the calculations again. In the second case, the equilibrium shifts to the left instead of the right, so the signs on all the x’s should be reversed (unless getting a negative value for x doesn’t bother you!). Doing variations on problems you have already worked helps you get the details straight, and also forces you to do your own consistency checks, so that you know your answers are correct.
Answers in books can be wrong, but answers you derive and check yourself are probably correct.
Example Removing some of the product C
Suppose we take the equilibrium from the last example and remove
d = 0.0300 M of component C. What are the new equilibrium concentrations?Solution Set up a new start-change finish diagram, and set
a = [A]0 = 0.0685 M, b = [B]0 = 0.0185 M and g - d = [C]0 = 0.1215 – 0.0300 M (leave this as g - d so we know where our numbers come from). The equilibrium will again shift to the right since we are removing C and the system will try to undo the change we made to it.| Component | A | B | C |
| Start | [A]0 = a | [B]0 = b | [C]0 = g - d |
| Change | - x | - x | + x |
| Finish | a - x | b - x | g - d + x |
Plugging this into the equilibrium constant, we get
![]()
Or
![]()
As before, we calculate each coefficient

And plug this into the quadratic formula
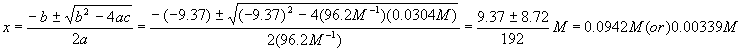
Again, we reject the first solution because it yields a negative (physically impossible) value for [A] and so
Let’s do a check to see that the numbers are realistic
![]()
Close enough.
By now, you might have noticed that the same reaction can yield algebra that looks very different, depending on the specific case. In reality, all these problems are closely related. Clearly the methods used in the last three examples are very similar, but there are details which differ from case to case. This is to be expected, and illustrates an important fact: unless you do plenty of examples so you can see the underlying unity in all these problems, your professor doesn’t have to change very much in the exam questions to trip you up. A wise student will take note of this and prepare carefully by varying each detail until all are under her/his control.

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students