
Technical Tutoring Home · Technical Tutoring Blog · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Keeping it Clean! · Amazon Fire Tablets, Kindle E-Readers and Accessories · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Ideal Gases
Ideal Gas Law · Density · Boyles and Charles Law · Ideal Gases II · Recommended Books
Of the three phases of matter, gases tend to exist at relatively high temperatures and low pressures. Decrease the temperature enough and the gas will condense into a liquid or sublime into a solid. Likewise, increase the pressure enough and condensation or sublimation will happen. Gases are different from solids and liquids (which are referred to as "condensed matter") in that there is room between the molecules. Typically, the space between molecules in the gas phase is large compared with the size of the molecules.
Consider a sample of gas inside a piston cylinder (a cylinder with one movable end cap so the volume inside the piston can be changed). The gas evenly fills the volume of the cylinder (the defining property of gases). If the piston is held at a fixed position, then the gas sample has the following important properties:
For the purposes of this discussion we will limit ourselves to measuring pressures in atmospheres. Later, we'll do some calculations with torr. There are many other pressure units in use, particularly pounds force per square inch (psi) and Pascal = Newton per meter squared.
For most gases at temperatures near (or above) room temperature (298 K = 25o C) and near (or below) room pressure (1 atm = 760 torr), the ideal gas law adequately describes the behavior of the gas:
![]()
Where R = 0.08206 L atm mol-1K-1 is a constant of nature called the ideal gas constant.
Example (standard temperature and pressure)
What is the volume (in L) of 1 mole of an ideal gas at standard temperature (273 K) and pressure (1 atm)?
Solution
Solve the ideal gas law for the volume and plug in the numbers
![]()
Example (find temperature)
0.105 moles of an ideal gas occupy 5.00 L at a pressure of 0.975 atm. What is the temperature of the gas in K and oC?
Solution
Solve the ideal gas law for the temperature and plug in the numbers
![]()
Which is the answer in K. To get oC, use the formula
![]()
Note: Temperatures in K can never be negative, but temperatures in oC can.
Example (find moles)
How many moles of an ideal gas take up 35L of volume at 25oC and 1.5 atm?
Solution
First, convert oC to K, 25 oC +273 = 298 K, then solve the ideal gas law for moles and plug in the numbers
![]()
Example (find pressure)
2.39 moles of an ideal gas at 300 K occupy 29.0 L. What is the pressure?
Solution
Solve for the pressure and plug in the numbers:
![]()
Gases aren't very dense compared to solids and liquids, but they still have a density. Density is defined as mass per volume, and the relation between mass and moles of course is the molecular weight, Mw. The reader may have noticed that in the examples above, we really didn't care which ideal gas we talked about, just that it was ideal. Usually with density calculations, we need to know what gas we are talking about so we can calculate its molecular weight and thus put mass into the calculation.
Recall the molecular weight of a sample of a chemical is defined as
![]()
Where Mw is the molecular weight in grams per mole (g mol-1), m is the mass of the sample and n is the number of moles. Solving this for the mass gives
![]()
Density is usually given the symbol r? (Greek rho), so from the definition
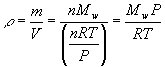
Example (density of an ideal gas)
What is the density of helium at room temperature and pressure?
Solution
Helium is a monatomic gas, so purists would insist that we say atomic weight rather than molecular weight, but we aren't going to be so finicky. From a periodic table, Mw (He) = 4.00 g mol-1. The pressure is 1.00 atm (standard room pressure) and the temperature is 298 K (standard room temperature). Plugging these into the density equation gives
![]()
Example (density of air at room temperature and pressure)
Air is approximately 21.0 mol % oxygen and 79.0 mol % nitrogen. What is the density of air at room temperature and pressure?
Solution
This is an example of a problem where we use the composition of the mixture of gases to come up with a "molecular weight" for the mixture. Since the two %ages above add up to 100 %, we can use their fractional equivalents to get an average molecular weight for the mixture of gases in a pretty obvious manner:
![]()
(beware - you cannot always do this - it depends on the specific situation). Plugging this number in gives
![]()
Note that air is 1.18 / 0.164 = 7.2 times denser than helium, which is why helium balloons rise in air.
Before and After: two different states of the same gas - Boyles and Charles Law
A very common problem in chemistry is to take a sample of gas, perform some process on it (like compressing or expanding it) and then ask what changed during the process. Before the process happened, the gas was in its initial state. After the process, the gas is in its final state.
Suppose we take the sample before we did the process and put "1" labels on every property of the gas:
![]()
Then do the process, and write the ideal gas law again, this time putting a "2" label on every property of the gas:
![]()
Now, solving for R on both sides,
![]()
This is a slightly generalized version of the equation in most chemistry books, which covers the case when even the moles are allowed to change. If the moles are constant,
in other words, when we are talking about the same sample of gas before and after (no addition nor removal of gas), then n1 = n2 and the equation is called the combined law of Charles and Boyle
![]()
Example (using combined Law of Charles and Boyle to find temperature)
We start with a sample of 13.2 L of ideal gas at 1.34 atm and 244K. If we compress the gas so the new volume is 5.43 L and the pressure is 1.88 atm, what is the new temperature?
Solution
We are looking for the temperature after the compression, so we solve the combined law for T2
![]()
Example (using combined Law of Charles and Boyle to find volume)
Using the same initial conditions as the previous example, what is the final volume if the final pressure is 3.11 atm and the final temperature is 323K?
Solution
Solve the combined law for V2 and plug in the numbers
![]()
A very similar calculation can be done for the case where the pressure is the number to be found.

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students