
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Antiderivatives and the Riemann Integral
Introduction · Derivatives and antiderivatives · Integrable functions · Indefinite integrals · Fundamental Theorem of Calculus: Use of indefinite integral to evaluate definite integrals · Examples · Comparison between the definition and the fundamental theorem of calculus (FTOC) · Recommended Books
In a previous article, we introduced the Riemann integral
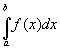
and developed a limit process for calculating it. We mentioned that the integral represents the area under the curve f(x) to the x-axis starting with x = a and ending with x = b, and stated without any support at all that the integral was the inverse operation to the derivative. We now take up this idea in detail, and supply some more technical groundwork for the theory of the integral.
Derivatives and antiderivatives
Elsewhere, we showed how to find the derivative f’(x) of a function f(x) at a particular point x = x0:
![]()
In practice, this definition can get difficult to use rather fast, so we derived an easier-to-use formula that works for powers of x only:
![]()
Although good only for polynomial functions, this is a very useful formula. Using the formula is equivalent to the operations: multiply by the power of x and then subtract 1 from the exponent. Were we to write this process as an operator acting on the function, we might define the operator as:
![]()
The operator acts on the nth-order polynomial function xn by multiplying by n the next smallest polynomial function xn-1. We bring up operators (naively, to be sure) to point out that there can then be an "inverse" operator Ix which reverses the action of the derivative operator Dx:
![]()
We can construct this operator intuitively by reversing the operations: add 1 to the power and then divide by the new power:
![]()
The constant C is required since we know derivatives destroy all constants; therefore the integral must create a constant. We don’t know what the constant might be, so it can be any constant, hence, we say C is an arbitrary constant.
If we apply the derivative operator to a function which has been integrated with the integral operator, we get

Applying the operators in the opposite order yields:
![]()
These operators are only inverse operators "up to a constant" – applying them in different order yields different results. For this reason, referring to the integral as the "inverse" operator to differentiation warrants quotes – integration is nearly, but not exactly, the inverse operation to differentiation.
It would be wise to note here that the results above apply not only to powers of x, but to any function that can be differentiated – the integration operation is only the inverse operation up to a constant. For other differentiable functions, the same effect noticed above is also true – integrating first, then differentiating produces the original function, but differentiating first, then integrating produces the original function and an added, arbitrary constant.
When we constructed the Riemann integral in another article, we said very little about which functions could be integrated using that technique. All we said was that the upper and lower integrals had to be equal in order for the function to be considered integrable.
In fact, this is sufficient to define the class of Riemann-integrable functions. Notice that nothing was said about continuity; in fact, there are many discontinuous functions that are Riemann integrable. This makes the class of integrable functions much larger than the class of differentiable functions, which not only require continuity, but a degree of smoothness (ie, no sharp "kinks" like in |x|) as well. This is another important difference between integration and differentiation – we can integrate functions we cannot differentiate. In fact, there are continuous functions that cannot be differentiated anywhere. In theory, any continuous function has a Riemann integral. Precise characterization of the class of integrable functions is beyond our present scope; suffice to say all differentiable functions are integrable.
In normal practice, we rarely, if ever, use the antidifferentiation operator Ix. Instead, when we need to talk about the integral of a function as though itself a function, we use the indefinite integral. There are two popular notations:

These are used in slightly different ways best learned by considering examples. Suppose we are again using the function f(x) = xn. The indefinite integral is then expressed as either
![]()
so that the "indefinite" part of the expression is the arbitrary constant C, or equivalently,
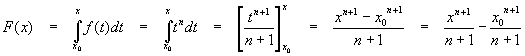
Equating the two results gives
![]()
The right-hand side of this last equation is just as arbitrary as the constant C, since the constant x0 is undetermined.
Fundamental Theorem of Calculus: Use of indefinite integral to evaluate definite integrals
When the limits of integration above and below the integral sign are numbers, the integral is called a definite integral and has a numerical value. We hinted above at how the integral is computed by evaluating the antiderivative at each limit and subtracting the results; explicitly, if we know the antiderivative
![]()
then the definite integral is
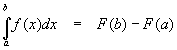
Returning to our example, for f(x) = xn,
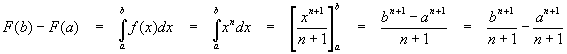
The arbitrary constant C subtracted out and so was ignored. We will always ignore the C when evaluating a definite integral, since this will always be the case.
This reduces computing the integral to:
Note that this formula does not work when n = -1!!! We shall examine this special case later.
Examples Integral of a Constant Function · Integral of f(x) = x · Integral of f(x) = x2
Example Find the integral of the constant function f(x) = c from x = 2 to x = 4.
Solution We found the answer to this in the "Construction of the Riemann Integral" for the special case c = 1. We can make this a bit easier by noting that a constant is just
the constant multiplied by the function x0 = 1, so:
![]()
Now, plugging in our limits allows us to evaluate the definite integral
![]()
Setting c = 1 as in the previous article gives the same answer as found before, 2.
Example Find the integral of x from x = 1 to x = 2.
Solution This example also appeared in the previous article, where we found the answer to be 3/2. Here, we first compute the antiderivative:
![]()
and then evaluate it between the two limits:
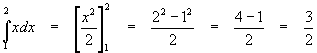
The reader can see that this method is clearly easier to use than the definition.
Example Find the integral of x2 between 0 and 1.
Solution Again, a repeat of an example given in the previous article. The antiderivative is
![]()
So the integral is
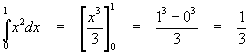
as was found before.
Comparison between the definition and the fundamental theorem of calculus (FTOC)
It is legitimate to ask, if the above is so much easier, why use the definition at all? Why not just use the FTOC all the time? The answer is somewhat complicated, but the essence is this: The FTOC allows easy evaluation of definite integrals, provided the antiderivative is known. We’ll use it when we can, and fall back on the definition when we must. While we have a convenient antiderivative formula for powers of x (and so for all polynomial functions by linearity), the class of functions we can and will be called upon to integrate is much larger than the class of polynomials. Learning new antiderivatives will become a regular part of studying a new function.
The definition, however inconvenient to use, is general, and will integrate all integrable functions (although considerable technique beyond what was covered may be required).
Like all convenient techniques, use of the FTOC is limited, specifically to functions we know how to antidifferentiate.
Calculation of antiderivatives for new, unknown, functions will be the subject of several articles. We will also learn how to use (antiderivatives of) known functions to find new antiderivatives with laws similar to the laws for finding derivatives of new functions from derivatives we already know.
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus
ã 1996 - 2002
Hyper-Ad Communications. All Rights Reserved.