
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
The Natural Logarithm Function
Introduction · Development of the function · Computation of the base · Notation: The Natural Logarithm · Summary of natural logarithm properties · Recommended Books
In another article, we discovered antiderivatives for powers of x, so that
![]()
We now deal with the exceptional case n = -1. The formula above for powers of x fails when n = -1 because there is a zero in the denominator. That is not the same as saying the function 1/x = x-1 has no antiderivative. We are looking for a function that will satisfy the requirement
![]()
In this case it is convenient to express our function as a definite integral:
Since the integrand (1/t) has t in the denominator, we cannot allow t = 0. We need the function to be differentiable (else it cannot be differentiated to give 1/x), so it also has to be continuous. These two conditions demand that t > 0, which automatically forces the limit of integration "a" to be greater than zero, too, since t takes on the value "a" when the integral is evaluated. Other than being greater than zero, the value of "a" is arbitrary. We can set it as we please and examine the results to see if the value will work for our purposes. The value can always be altered later if needed. This being the case, we might as well set a = 1.
With this constant set, we now have
![]()
and several properties of the new function come to light. First,
![]()
This is evident by the Fundamental Theorem of Calculus, since if L(t) is the antiderivative,
![]()
This is a direct consequence of our setting a = 1. Had we chosen any other value for "a", we would have simply changed the position of this zero of our function to "a" instead of 1. So our choice a = 1 has determined the zero of the function, which is acceptable.
Now, for t > 0, 1/t > 0, so as we integrate 1/t from 1 to some value larger than 1 (ie, find F(x), x > 1), the integral is positive (both the height of the rectangles and the width are positive) and increasing (the more positive area we include, the larger the integral). On the other hand, if we put a value in for x that is less than 1 (but greater than zero – see above), the height of the rectangles are still positive, but the widths are negative since they are headed in the negative direction, down from 1 to a smaller value. Thus, values of F(x) in the range 0 < x < 1 will be negative.
These facts can be summarized as further properties of our function:
We will prove elsewhere the result for any integrable function f(x)

(although it can be verified intuitively by drawing a curve and three points a, b and c along the x-axis). We use this result to look at what happens when we plug in a product
for x, say x = wy:
We can consider the last integral to be a function of y:
Note that
![]()
so L(y) has the same derivative as F(x) (only the form matters; to verify this, put y = x).
In fact,
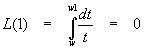
This shows that L(x) is the same function as F(x), since two functions with the same derivative everywhere differ by at most a constant; if the functions have a single point in common, the constant is zero and the functions are equal. In particular, L(y) = F(y) and so

Since this is true, we can find w > 0 and y > 0 so that w = 1/y and wy = 1, in which case
![]()
or
![]() .
.
Another consequence of this is that
![]()
Using the multiplication formula derived above, set w = y = x to get
![]()
Repeated applications of this give
![]()
regardless of the sign of n. In other words, it is also true that
![]()
Now suppose q is an integer and p = 1/q. Then pq = 1 and
![]()
Therefore our power rule is also good for rational numbers, so in general, if m and n are integers with n nonzero,
![]()
One might ask whether a similar rule holds for irrational numbers. The answer is yes:
If r is an irrational number, then there are rational numbers arbitrarily close to it. Suppose {rn} is an infinite sequence of rational numbers so that
![]()
Then, by continuity of F(x) we must have
![]()
The reader should note that we have derived a great many properties of the function F(x) without knowing anything about the actual form of the function. This type of reasoning is called functional, the equations derived are functional equations. We will use this type of argument for functions which cannot be easily be expressed in closed form (in other words, explicitly as a function of x).
Astute readers will recognize F(x) as a logarithm of some kind. We need only establish the base of the logarithm to completely characterize this function. We know from base 10 logarithms learned in high school that
![]()
So, whatever our base is, if we set the function value to 1, we should have the argument as the base. In other words,
![]()
makes b our base. To actually find this number, we will need to appeal to the definition of the integral and do some calculations. We know that F(x) is an increasing function, positive for x > 1, so it makes sense to use the lower integral definition to try to get b.
We have
![]()
As before,
![]()
This means
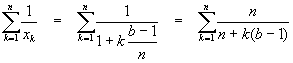
Plugging this in for the sum above gives us

This equation is too difficult to solve directly, but a numerical calculation using a computer (n = 1000, error at 0.01%) found that
b = 2.719 +/- 0.001
Close enough for our purposes. The actual number is called e, and is a classic, well-known irrational number that appears very, very often in calculus. The value of e to many decimals is
e = 2.71828182845904523536028747135266249775724709369995...
We will always refer to this number as e, the natural logarithmic base.
Note: The above calculation is a rather poor way to find e. The only advantage to the method used here is that we used techniques found either in this present article or in the article on "Construction of the Riemann Integral". In particular, it is not expected at this point that readers can just grab a computer and program a solution to a numerical problem like the one above.
Modern calculators are equipped to do simple numerical calculations (the author used them in undergraduate school c. 1978-1983), so some readers undoubtedly can try the numerical calculation if they like. At this point, other issues seem much more important.
Notation: The Natural Logarithm
Math texts use two different notations for natural logarithm; if the authors wish to avoid confusion with base 10 logs they will most likely use the notation
![]()
On the other hand, pure mathematics texts rarely need any type of logarithm other than the natural logarithm, and will assume implicitly that the natural logarithm is used. These texts will tend to use the notation
![]()
The notation "ln x" refers only to the natural log; the notation "log x" can mean either log base 10 or log base e (or some other base, but this is uncommon). Normally, the author will put a comment somewhere when using the "log" notation to avoid confusion, but this is not required and is sometimes assumed. We will use the "ln x" notation and avoid confusion.
Summary of natural logarithm properties
Let x and y be positive real numbers, z a real number:
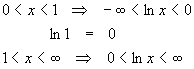 Domain and Range
Domain and Range
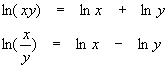 Multiplication and Division
Multiplication and Division
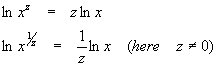 Exponentiation
Exponentiation
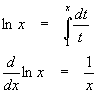 Calculus
Calculus
 Schaum's Outline
of Calculus (Schaum's...
Schaum's Outline
of Calculus (Schaum's...
 Schaum's Easy
Outline: Calculus
Schaum's Easy
Outline: Calculus
ã 1996 - 2002
Hyper-Ad Communications. All Rights Reserved.